In the world of mathematics, the sequence of numbers that will always have a constant difference between the consecutive numbers will always help in representing the concept of arithmetic sequence very easily. For example, the arithmetic sequence will be 4, 8, 12, 16 and 20 and the common difference between all of them will be 4. In any kind of arithmetic sequence, people simply need to add or subtract the same number to reach and make the sequence in the whole process very easily and efficiently.
The sequence is a set of numbers which will be in a particular order and the sequence can be anything like a sequence of cards, sequence of letters and several other kinds of related things.
It is very much important for people to be clear about the formula of the arithmetic sequence to avoid any kind of chaos and the following are the basic things that people need to know about this particular concept:

If the individuals are interested in finding out the 25th odd number of the sequence or to find out the sum of the first 50 odd numbers then they need to use the right kind of arithmetic sequence formula or otherwise it will take a lot of time to find out the exact value. The arithmetic sequence formula has been written as:
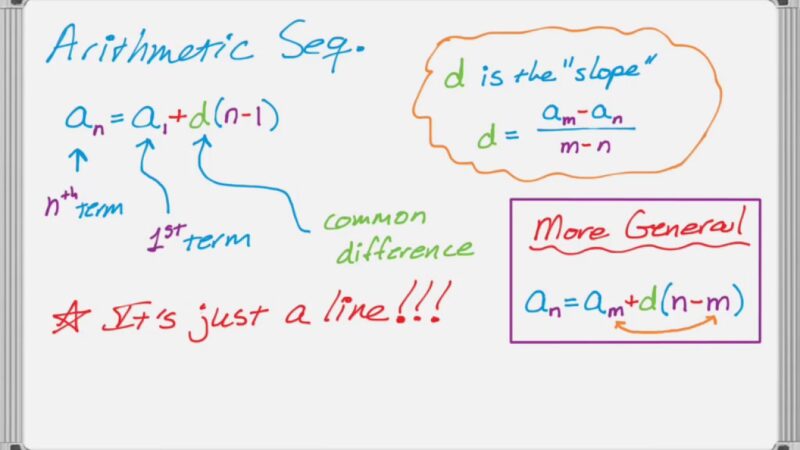
- PN = P1 + N -1 into D. In this particular case PN is the NTH term, P1 is the first term and D is the difference between the consecutive numbers and N is the position of the terms. This formula can be perfectly referred to as finding out the concept of the NTH term formula of the arithmetic progression.
- If people are interested to find the sum of first N numbers into the arithmetic sequence then the following formula has to be used which will be SN = N/2 into 2P + and -1 into D. In this particular case, SN is sum of N terms, P is first term and D is difference between consecutive numbers.
- To calculate the difference of first N terms into the arithmetic sequence of the following formula has to be used which is D =PN – (PN -1). In this particular case, D is the difference of N terms, PN is NTH term and PN -1 is the previous term of the PN.
- Finding the sum of the arithmetic progression in this particular case is very much important so that everybody will be able to have a clear idea about the basic technicalities. The formula over here will be SN = N/2 into P1 + PN. In this particular case, P1 will be the first term and PN will be the last time and SN will be the sum of the first and the last term.
An example of arithmetic sequence has been explained as follows:
- Finding out the 25th term of the arithmetic sequence of 2, 5, 8 and 11 have been explained as follows:
- Solution: Finding out the NTH term of the arithmetic sequence will always be based upon utilization of the basic values and for this particular purpose calculation will come out to be as P1 will be 2, D will be 5-2=3 and end value will be 25. So, implementation of the values in this particular formula answer will come out to be 74 and hence people can state that the 25th term of the sequence would be 74.
Hence, to become a master of this particular topic people need to attend the math classes at platforms like Cuemath so that they can have a good hold over the basic calculations and technicalities.

